NewsKing.org

	The Monty Hall Problem

	by T.J. Newton

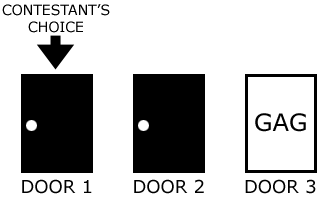
The "Monty Hall Problem" is a statistics problem inspired by the game show "Let's Make A Deal," which was hosted by Monty Hall in the 1960's, 70's, and 80's. In many of the shows, the contestant was asked to "choose" or "bet on" one of three closed "doors," behind which there may have been either a prize or a gag. It has been assumed that there was always only one prize, and two gags. In this example, let's say that the contestant chooses door number one. Monty would then reveal what was behind either door number two or three. It has also been assumed that Monty always reveals a gag. Let's say Monty reveals what is behind door number three, and that it is a gag. The contestant is then asked to either stay with their choice (here, door number one) or change their bet (to door number two, in this example).

The Monty Hall Problem concludes that two out of three times, the contestant is better off changing their bet (to door number two) than they are staying with their original bet (door number one). In other words, according to the Monty Hall Problem, the contestant who changes their bet wins 2/3 of the time.

Most people who disagree with the conclusions of the Monty Hall Problem will probably like the "fireman example." The "fireman example" states that if, at the right moment, another (non-observing) contestant enters the room, he or she will have a 50|50 shot.

Let's assume that after door number three is revealed and the contestant is asked to change their bet or stay with their original choice, the fire alarm goes off. The contestant runs off and is never seen again. The alarm turns out to be some burnt popcorn, so Monty asks a firefighter to choose between door number one or door number two to win a prize a or a gag. The firefighter has a 50|50 shot.

In other words, changing your bet seems like flipping a coin. When you are asked whether or not you want to change your bet, the "choice" you make seems like a 50|50 shot. In fact, if you were to flip a coin to decide whether or not to change your bet, your odds of winning would be 1/2 (or 50|50). So people who disagree with the conclusions of the Monty Hall Problem have a point. But when your odds are calculated based on the original game in play, you have a 2/3 chance of winning if you change your bet, and 1/3 chance of winning if you keep your bet.

So, you flip a coin and decide that if the coin lands on heads you change your bet, and that if it lands on tails you stay with your original bet. If the coin lands on heads you have a 2/3 chance of winning, and if the coin lands on tails you have a 1/3 chance of winning. But since the odds of the coin landing on either heads or tails is 1/2 (or 50|50), your overall chances of winning or losing are 50|50 if you flip a coin...

Here's another way of looking at it:

Change = 2/3 (Win); 1/3 (Lose)
Stay = 1/3 (Win); 2/3 (Lose)

Heads = 1/2
Tails = 1/2

Heads = Change
Tails = Stay

Win + Win = 3/3
Lose + Lose = 3/3

1/2 x 3/3
----------- = "50|50"
1/2 x 3/3

Here is some of the information above displayed in a table:

Monty Hall Table

---	Win	Lose
Change (Heads)	2	1
Stay (Tails)	1	2
*Total*	3	3

You could also do it this way:

(1/2 x 2/3) + (1/2 x 1/3)
----------------------------- = "50|50"
(1/2 x 1/3) + (1/2 x 2/3)

I feel like I just beat the matrix (statisticians solve these problems with "matrices"). So I want to be clear; if you flip a coin you change your odds...

If you're still not convinced, you can click HERE to try all this out for yourself. Dr. R. Webster West has a simulation of the Monty Hall Problem on his web page. Try the simulation and flip a coin to decide whether or not to change your bet. Here are some sample results for flipping a coin:

In 13 games in which you have switched, you have won 8 times.
In 13 games in which you have not switched, you have won 5 times.

This means you have played a total of 26 games (13 + 13 = 26) and won a total of 13 times (8 + 5 = 13). 13/26 is exactly 1/2, or a 50% rate of winning and a 50% rate of losing, which equals 50|50. The results also indicate that your coin came up "heads" 13 times and "tails" 13 times, which makes sense if you flip the coin a total of 26 times.

Switching your bet won 8/13 times. 8/13 is as close to 2/3 as you can come if you switch your bet 13 times.

Staying with your orginal bet won 5/13 times. 5/13 is almost as close to 1/3 as you can come if you stay with your original bet 13 times.

The results will not always match the calculated odds perfectly, but the more games you play, the closer the results will be to the calculated odds. You should come pretty close if you play 1000 games (1).

If you are interested in more information (background, formulas, etc.) click HERE for Wikipedia's article. You can also check out Michael Shermer's dialogue with someone who wrote to Scientific American about Shermer's October 2008 SciAm article on the Monty Hall Problem.

Notes

1) A Monte Carlo Analysis can be used to calculate the exact number of games needed to achieve a specified margin of error. Dr. Daniel Ellard has calculated that flipping a coin 384 times will yield "heads" 50% of the time, accurate to within 5%, with a 95% level of confidence. Dr. A.M. Garsia has a Monte Carlo Simulation of the Monty Hall Problem that allows people to experiment with different numbers of games without actually having to play the game themselves.

Gift Shop


	Shopping at NewsKing.org is easy. Just click "Add to Cart" to select an item, and a shopping cart window will open. Major credit cards, eCheck, and PayPal accepted.


NewsKing.com Bumper Stickers - "Protect Your Free Will" text. Vinyl won't fade or crack. View Image - 3/$18.00




Website CD-ROM - Get everything from all four websites on CD-ROM, plus exclusive bonus features. - $39.00




Donate Now! - Make a contribution to NewsKing.org today and help make tomorrow's journeys possible.

Feedback

Feedback will remain anonymous unless you specify your email address here:
email (optional)

How did you like the presentation?
I liked it.
I thought it was okay, not great.
I didn't like it.

Was the presentation clear and understandable?
It was crystal clear.
It was a little hazy.
It was covered with a dense fog.

Comments:

(To reload the image without Javascript, use the Reload button in your browser instead.)

Enter the Security Code displayed above:

Feedback, including comments entered above, will remain anonymous unless you specified your email address.
THANK YOU!

Selected Works Cited from Internet

Shermer, Michael. (2008). Scientific American, Feb. 2009. "The Monty Hall problem" http://www.sciam.com/article.cfm?id=the-3-door-monty-hall-problem, 28 Jan. 2009.

West, R. Webster. The let's make a deal applet. http://www.stat.sc.edu/~west/javahtml/LetsMakeaDeal.html, 28 Jan. 2009

Wikipedia. Monty Hall problem. http://en.wikipedia.org/wiki/Monty_Hall_problem, 28 January 2009.

About This Site/Disclaimer